Density Current Paper, 1996 by Xue, M., Q. Xu and K.K. Droegemeier

Density Currents in Two-layer Shear Flows

Ming Xue

CAPS, University of Oklahoma, Sarkeys Energy Center,

100 East Boyd, Norman, OK 73019.

(Submitted to the Quarterly Journal of Royal Meteorological Society 1999)

Summary

In this paper, a previous two-fluid model of idealized density current in low-level shear is extended to include variable upper-level shear. Far-field solutions are determined based on the conservation of mass, momentum and vorticity and the conservation of Bernoulli function (energy) along streamlines for inviscid flows. It is found that the upper-level shear plays a similar role as the low-level shear in controlling the depth of steady-state density currents. In most cases, large positive upper-level shear supports deeper density current and steeper front therefore stronger updraft. It is also found that when the low-level shear is weak and upper-level shear occupies about half of the domain depth, larger positive shear can result in a shallower rather than deeper density current. This behavior was not found for either constant shear flow or flows with only low-level shear. The behavior is understood by examining the flow structure and flow-force components as a function of the upper-level shear. Furthermore, by allowing the upper-level shear to vary, an overturning flow is permitted ahead of the density current. This is not possible in the earlier model in which the upper-level flow is assumed to be constant. This extension allows us to draw closer analogues between the current solutions with the circulation patterns found in typical squall lines in sheared environment.

Time-dependent numerical experiments are conducted for a range of upper and low-level shears. The depth and the propagation speed of simulated density currents are found to agree very well with predictions by the idealized theoretical model. This verifies the validity of the theoretical model. In addition, numerical experiments with identically zero low-level shear but differing upper-level shears suggest that the deeper shear is as important as the low-level shear in determining the uprightness of the upward branch of inflow. In fact, the presence of positive low-level inflow shear may not be essential. Such results are also supported by the theoretical model and may have important implications to our understanding of squall line dynamics.

The full length paper and figures are at this ftp site.

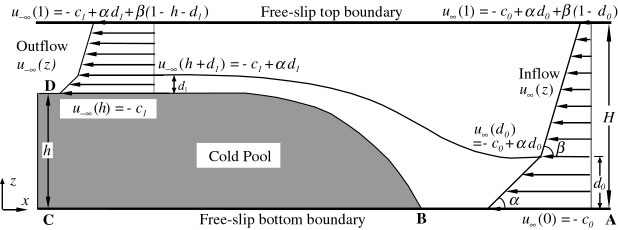
Figure 1. Schema of the steady-state model of a density current circulation in an environmental flow with low-level shear.

Experiment D2L01a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L05a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=0.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L09a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=-2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L11a. Low-level shear alpha=0, layer depth=0.2, upper-level shear beta=2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L19a. Low-level shear alpha=0, layer depth=0.2, upper-level shear beta=-2. Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L01a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L05a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=0.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L09a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=-2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L11a. Low-level shear alpha=0, layer depth=0.2, upper-level shear beta=2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L19a. Low-level shear alpha=0, layer depth=0.2, upper-level shear beta=-2. Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L01a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24. Click on the picture for java animation.

Experiment D2L05a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=0.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24. Click on the picture for java animation.

Experiment D2L09a. Low-level shear alpha=1, layer depth=0.2, upper-level shear beta=-2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24. Click on the picture for java animation.

Experiment D2L11a. Low-level shear alpha=0, layer depth=0.2, upper-level shear beta=2.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24. Click on the picture for java animation.

Experiment D2L19a. Low-level shear alpha=0, layer depth=0.2, upper-level shear beta=-2. Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24. Click on the picture for java animation.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.

Experiment D2L19a. Low-level shear alpha=0, layer depth=0.2, upper-level shear beta=-2. Predicted density current depth = 0.59, simulated current depth=0.54). Shown in the figure are buoyancy contours and wind vectors at non-dimensional time 24.
Click on the picture for java animation.