Introduction
A vectorised code can run a degree of magnitude faster than a non-vectorised one on a Parallel Vector Processor (PVP) system such as the Cray J916 Supercomputer. Most users expect the compiler to do automatic vectorisation for them regardless of how their codes were written. Unfortunately, that does not happen all the time. In many cases, manual work is needed on the part of the coder to achieve maximum performance. Before embarking on vectorising your code, it is necessary to understand what is vector processing.
Vector Processing
Suspend your long-held notions of vectors acquired from your school day linear algebra lesson! A vector here is defined as an ordered list of scalar values. A simple vector in a computer's memory is defined as having a starting address, a length (number of elements), and a stride (constant distance in memory between elements). For example, an array stored in memory is a vector. Vector systems have machine instructions (vector instructions) that fetch a vector of values from memory, operate on them and store them back to memory. Basically, vector processing is a version of the Single Instruction Multiple Data (SIMD) parallel processing technique. On the other hand, scalar processing requires one instruction to act on each data value. Here are the comparisons:
DO 100 I = 1, N
A(I) = B(I) + C(I)
100 CONTINUE
If the above code is vectorised on the Cray J90, the following processes
will take place,

And, if the code is not vectorised on the Cray J90, the following scalar processes will take place,
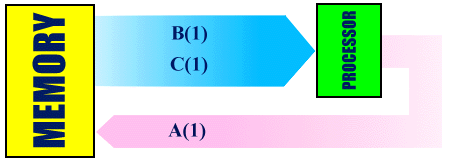
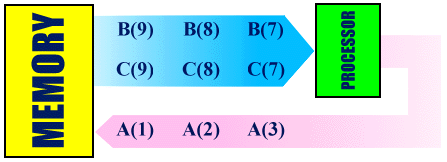
Vector processing allows a vector of values to be fed continuously to the vector processor. If the value of N is large enough to make the start-up time negligible in comparison, on the average the vector processor is capable of producing close to one result per clock cycle. If the same code is not vectorised on the Cray J90, for every I iteration, e.g. I=1, a clock cycle each is needed to fetch B(1) and C(1), about 4 clock cycles are needed to complete a floating-point add operation, and another clock cycle is needed to store the value A(1). Thus a minimum of 6 clock cycles are needed to produce one result. We can say that there is a speed up of about 6 times for this example if the code is vectorised.
Here is an example where a speedup of more than 10 times can be achieved through vector processing,
DO 200 I = 1, N
A(I) = B(I) * C(I) + D(I)
200 CONTINUE
If the above code is not vectorised, more than 10 clock cycles will be
needed to produce a single result on the Cray J90. However, a vectorised version
will still generate approximately one result per clock cycle. The chaining
feature available in the vector processor enables the results generated by the
multiplier to be fed continuously to the adder, and allows the multiplier and
adder to operate concurrently. Vector operations like add and multiply are done
in a vector pipeline in the processor. The examples given above contain codes
which are inherently vectorisable. But in reality, not all codes are
vectorisable, at least not all are readily vectorisable.
Characteristics of Vectorisable Code
The two previous examples have illustrated a number of important points in vector programming. Vectorisation can only be done within a DO loop, and it must be the innermost DO loop. It is crucial to ensure that there are sufficient iterations in the DO loop to offset the start-up time overhead. As shown in the above two examples, to tap as much power as possible from the chaining feature, one should try to put more work into a vectorisable statement (by having more operations) to provide more opportunities for concurrent operation (However, there is a limit to it, the compiler may not vectorise the code if it is too complicated). Having a DO loop is by no means an assurance of vectorisation. The existence of certain codes in the DO loop may prevent the compiler from converting the entire or part of the DO loop for vector processing. They are collectively known as the vectorisation inhibitors. To ensure greater vectorisation, a programmer will have to avoid putting vectorisation inhibitors in the DO loop or to reconstruct the DO loop by replacing vectorisation inhibitors with an equivalent code which enable vectorisation.
What is a Vectorisation Inhibitor?
Recursive data dependencies is one of the most 'destructive' vectorisation inhibitors. Recursion occurs when any address set in one iteration of a DO loop is referenced in another iteration. Single-dimension recursion, as shown below, will prevent any vectorisation of arithmetic operations in a DO loop.
A(I) = A(I-1) + B(I)The correct computation requires the values of A(I) to be updated before they are used in the next iteration. If the above code were to be forcibly vectorised (this can be done by using vector directives, more will be discussed later), all the old values of A(I) would be fetched from memory by the vector instruction before any new values had been updated. This generates incorrect results.
Other commonly found vectorisation inhibitors include subroutine CALLs, references to external functions for which the compiler knows of no vector version (some vectorised arithmetic functions are available on the Cray system), any input/output statements, assigned GOTO statements, certain nested IF blocks and backward transfers within loops. Inclusion of some of these vectorisation inhibitors in a DO loop prevents the compiler from having a full picture of the computation flow. For example, during compilation, the compiler does not know how the subroutines and the external functions are related to the calling program, hence preventing it from vectorising the DO loop. These types of inhibitors can be removed by expanding the function or inlining subroutine at the point of reference. If the DO loop satisfies the conditions for vectorisation after in-line expansion, it will be vectorised. In fact, there are many other restructuring techniques that can be used to increase the degree of vectorisation. A very good reference on this can be found in A Guidebook to Fortran on Supercomputers by John M. Levesque and Joel W. Williamson.
Vectorisation Directive
In some cases, the compiler may not vectorise a particular code even though it is vectorisable. This happens when the compiler is unable to determine whether the correct relationship between definition and reference will be maintained, for example,
DO 300 I=1,N
IX(I) = IA(I) - IB(I) * IC(I)
300 H(IX(I)) = H(IX(I)) + 1.0
At compile-time, the compiler does not know what the values of
IX(I) are going to be. If some values among the N values from
IX(I) to IX(N) were the same and the DO loop were to be
vectorised, incorrect results would be generated. However, if you are sure that
all N values from IX(I) to IX(N) are different, you can add
the following vectorisation directive immediately before the loop to indicate
that recursive data dependency does not exist in the loop. This will
subsequently enable the compiler to vectorise the above DO loop.
CDIR$ IVDEP (Note: The above directives are Cray specific. M. Xue)The above vectorisation directive statement starts at the first column therefore making it portable as other compilers will treat it as a comment line. Vectorisation directive can also be used to prevent vectorisation of certain DO loops when the overhead exceeds the benefits of speed-up. Basically, a vectorisation directive makes automatic vectorisation by the compiler more efficient by providing information which the compiler cannot gain from its own analysis of the source program.
Automatic Vectorisation by Compiler
The following options can be used to activate automatic vectorisation by the Fortran compiler:
cf77 -dp -Zv myprogram.f
or
cf77 -dp -Ovector3 myprogram.f
(Note: Compiler options for cray fortran 90 compiler f90 can be found from man pages. Do man f90 on J90. M. Xue).
The -dp option forces all variables (both single and double precision) to be processed as 64-bit variable. In the Cray system, single-precision variables are 64 bits long while double-precision ones are 128 bits. If you do not need precision of more than 64 bits, the -dp parameter ensures that your program will run many times faster without having to modify the source code.
Performance Monitoring Tools
Before taking up the challenge of optimising your program further, you need to know how well your program is running at the moment. There are a number of tools you can use to monitor various performance aspects of your program such as the level of vectorisation and the I/O and memory performance, and to identify the compute intensive section of your program. Such information will help you to decide the type of optimisation techniques you need to apply and where to focus your efforts on.
If you need any assistance in code optimisation, please do not hesitate to contact us at ccesvuhelp@nus.edu.sg.
Source of this page: http://www.nus.edu.sg/Major/SVU/techinfo/vector_processing.html